A post about some maths homework caused some consternation and confusion on one of my local facebook groups:

Lots of people seemed to think this was far too advanced for a 9-year-old, or that solving such puzzles would have no applications in real life.

I beg to disagree.

Yes, I admit that solving the puzzles takes a sizeable number of steps, and might test the concentration of your little ones, but the steps themselves are easy to understand and easy to execute. They do require a decent understanding of numbers though.

The underlying principle of solving any maths equation is to use the known facts to derive other things which we can treat as new facts. And then using those facts to derive even more stuff.

In other words: Common sense. You can formalise this into propositional calculus, first-order logic or whatever you like, but at the end of the day it is common sense. Or rather: common sense on stereoids.

In this sense, the puzzles presented to the 9-year-olds are less about formal maths than general problem solving: Using what you already know to figure out stuff. Which then allows you to figure out more stuff. Rinse and repeat ad nauseum. Surely this is something an education system is meant to do!

It was presented on facebook without much context, but there are some reasonable assumptions to make here:

• each letter represents a single digit

• two-digit numbers are represented as two letters. This is contrary to the normal maths notation where there would be an implicit multiplication

• In each table, each letter stands for a different digit. No two letters stand for the same digit within the same table.

• With only 9 distinct letters in each table (except for Table Y), some digit must be left out - we do not know which one, but zero sounds like a reasonable guess. Nobody likes zeros anyway. They don't matter.

• The goal of the puzzle is to figure out which letters represents which digits

A quick refresher on notation:

• The $\Rightarrow$ symbol should be read as "implies that". So $A \Rightarrow B$ can be read as "A implies B": If A is true, then B is also true. And if A is false, then B is also false.

• $\times$ is the multiplication symbol. But you did know that, right?

Table W

This is the easiest one to solve - it's basically a taster:

With the assumptions above, we can focus in on $H \times H = H$ : this means $H$ can only be zero or one, no other numbers are possible. And since e.g. $H \times A = A$, this means that $H$ cannot be zero. Hence $H = 1$.

And that's it! The remaining letters can represent whatever digits you like (including zero), and the equations will all be true.

Table X

Here we step up the difficulty level slightly:

Yes: the authors skipped the letter E for some reason....

From $D \times A = D$ we can conclude that $A = 1$.

And considering $D \times D = JA \Rightarrow D \times D = J1$ : So $D$ times itself must result in a two-digit number whose last digit is $1$ : The only possiblity here is $D=9, J=8$

Plugging in those values into the remaining equations revals the value of some more letters:

$D \times I = AJ \Rightarrow 9 \times I = 18 \Rightarrow I = 2$

$D \times J = HI \Rightarrow 9 \times 8 = H2 \Rightarrow H = 7$

We can then use the newly found value of $I$ and $H$ in one of the other equations:

$D \times C = IH \Rightarrow 9 \times C = 27 \Rightarrow C = 3$

$D \times H = FC \Rightarrow 9 \times 7 = F3 \Rightarrow F = 6$

$D \times F = BG \Rightarrow 9 \times 6 = BG \Rightarrow B=5, G=4$

And we then know the values of all the letters - even though we haven't "used" all the equations yet.

Table Y

Here we step up the difficulty level even futher. We have 10 letters, but still only 9 equations:

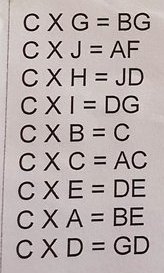
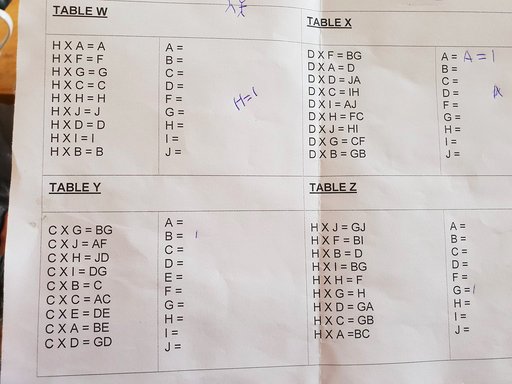
From $C \times B = C$ we can conclude that $B = 1$. Yes, the devious teachers hid it in the middle, rather than presenting it as the first equation! They expect you to understand the principles by now!

But then it gets slightly trickier...

Consider $C \times C = AC$ : The square of $C$ is a two-digit number with $C$ as its last digit. Hence $C = 5$ or $C = 6$, but we do not know which one yet.

If we were to guess at $C = 5$, then the last digit of any of the products must be either $0$ or $5$ - which is not the case (we would only see two possible values as the right-most digit on the right-hand side of the equations, but there are obviously more than that). Hence, $C$ cannot be $5$ after all. So it must be the case that $C = 6$.

If $C = 6$ and $C \times C = AC$ then $A = 3$.

As before, we can take the values we know so far and plug into one of the remaining equations to develop more knowledge:

$C \times A = BE \Rightarrow 6 \times 3 = BE \Rightarrow 6 \times 3 = 18 \Rightarrow B=1, E=8$

$C \times E = DE \Rightarrow 6 \times 8 = D8 \Rightarrow D = 4$

$C \times D = GD \Rightarrow 6 \times 4 = G4 \Rightarrow G = 2$

$C \times I = DG \Rightarrow 6 \times I = 42 \Rightarrow I = 7$

which leaves F, H and J as unknowns and no letters (yet) representing 0, 5 or 9. And these two equations are yet to be solved:

$C \times J = AF \Rightarrow 6 \times J = 3F$ : So $J$ has to be either $5$ or $6$ making $F$ either $0$ or $6$. But we already have a letter for $6$ ($C$), which leaves only the possibility of $F = 0$ which implies that $J = 5$.

Which leaves the last equation:

$C \times H = JD \Rightarrow 6 \times H = 54 \Rightarrow H = 9$

Table Z

In this table we're back to 9 letters (for some reason the authors decided to miss out on the letter E again!??) and 9 equations:

As before, from $H \times G = H$ we can conclude that $G = 1$.

Plugging $G = 1$ into the first equation gives:

$$H \times J = GJ \Rightarrow H \times J = 10 + J$$

... after subtracting $J$ from both sides of the equation:

$$(H-1) \times J = 10$$

And since the only factors of 10 is 2 and 5, then one of the following must be true:

• $(H-1) = 2$ and $J = 5$, i.e. $H = 3$ and $J = 5$
• or $(H-1) = 5$ and $J = 2$, i.e. $H = 6$ and $J = 2$

... but we do not yet know which one.

We also have the equation $H \times H = F$ - so $H$ must be either 0, 2 or 3 (it cannot be 1, since $G = 1$). Any higher numbers would result in $H \times H$ ending up as a two-digit number. And then we can exclude $H = 0$, as then we should have expected an $H$ on the right-hand side of the equation.

So it must be the case that $H = 3$, as this is the only value which can satisfy both the previous 2 paragraphs!

And since $(H-1) \times J = 10$, then $J = 5$

$H \times H = F \Rightarrow 3 \times 3 = F \Rightarrow F = 9$

$H \times F = BI \Rightarrow 3 \times 9 = BI \Rightarrow B = 2, I = 7$

$H \times B = D \Rightarrow 3 \times 2 = D \Rightarrow D = 6$

$H \times I = BG \Rightarrow 3 \times 7 = 2G \Rightarrow G = 1$

$H \times D = GA \Rightarrow 3 \times 6 = 1A \Rightarrow A = 8$

$H \times A = BC \Rightarrow 3 \times 8 = 2C \Rightarrow C = 4$

... and before we know it, it is solved!